Tag: diamond-square

Randomness is nice, except when you have too much.

It’s easy to blast random pixels all over the screen, but it’s much nicer when there’s some continuity in the randomness.

For diamond-square interpolation, I was looking for a way to generate (and use) random seed values to produce continuous-looking results within and between calculated tiles, as well as varying these seed values over time in a somewhat appealing fashion.

To calculate the values for a given tile requires the corner values of that tile along with the corner values of the eight surrounding tiles — that is, all the blue pixels in the picture are needed to calculate the pixels required to calculate the pixels in the centre tile.

The corner values from one tile effects the calculation of the tiles adjacent.  For this reason, the corner values of each tile are state that must remain constant for the entire frame.

To render a full 1920×1080 frame, 15×9 tiles are required, with 16×10 corner values.  To calculate the tiles around the frame border, further un-rendered tile data is required to correctly seed each of these border tiles.  The result of this is that 18×12 random pixel values are needed to define the full set of tiles for a 1080p frame, which means the seeds for the tiles of a frame can be stored in 18x12x4 = 864 bytes.  Not unreasonable.

When rendering each tile, these seed values are first placed in the appropriate 16 locations (taking into account the compressed outer regions), and the interpolation takes place.  (Interpolation is performed on the seed values and, later, using only values calculated during a previous iteration — which means there’s no requirement to zero memory between tiles)

The result with just this looks quite reasonable (imho) — there’s decent interpolation of random values across the screen.  These random seed values can also be permuted without too much difficulty between frames — I’ve tried some trig-function based methods to give a sense of continuous, directional changes.  It works but I’m sure there’s better options.

As for the random perturbing of interpolated values, I’ve tried a few methods and not achieved anything that I’ve been all that happy with.  The problem I’ve had is finding/generating a suitably random value of appropriate scale, and applying it to the pixel value fast enough.

(As I reach the end of this, I have the impression that what I’ve put together is almost, but not entirely unlike, Perlin noise —  you could possibly say that it has a really clumsy interpolation function.  I have a much better understanding of Perlin noise than when I began, and it really looks like I should have tried that.  Learning is Good.)

At some stage in the not too distant future, I hope to perform some screencaps and post some actual images and maybe even a video.  And fwiw I’ll post the source code, too.

There’s a hole in my dataset, dear MFC, dear MFC…

There’s a block of local store that holds a tile of pixels that need to be DMAd out to main memory.  128 lines makes performing many smaller transfers more complex , so we’ll try DMA lists why not.  The problem here is that the pixel data for each line does not match up directly with the next — between each is stored the extra lines of extra-tile information that was needed for the calculation.  When using DMA lists to transfer data to many memory, the source for each DMA transfer starts where the previous one ended. This means that between each DMA there’s (148-128)×4=80 bytes of information that we don’t want to see on the screen.

There’s a lot of things that are “best-practice” for SPU DMA, particularly relating to size and alignment of transfers, and I’m typically a religious adherent.  In this case, I did not comply with best practice and still met my time budget and only feel a small amount of shame :P

Overall, less time is spent performing DMA than is spent calculating pixels, so further optimising DMA for this particular program is unnecessary.

When transferring tiles from the SPU to the framebuffer, there’s three cases of particular interest:

1. Tiles on the right edge of the screen
2. Tiles on the lower edge of the screen
3. The Other Tiles

3. The Other Tiles

These are the easy ones.  They will never need to be trimmed to fit the screen edges, and if drawn in the right order have the wonderful characteristic that the extra data needed can be DMAd to the framebuffer and will be overwritten by pixel data from a later tile.  There’s no special case needed, just draw each pixel line and — all data between pixel lines — to the screen.

(For the diagrams, the amount of overdraw is far greater than the actual tile part — this is a consequence of the small size.  It’s a much smaller percentage for 128 pixel tiles.  I’ll post some actual screengrabs here sometime…)

1. Tiles on the right edge of the screen

Overdraw isn’t the answer in this case. It is not possible to overdraw on either the left or right of the rightmost tile in a way that will be correct when the screen is finished.  Instead, the extra information (including any portion that may not fit onto the visible screen) must be dealt with some other way.

My solution, ugly as it is, is to write each surplus portion of a tile to a scratch location in memory — every one of them to the same location.  It works :|

2. Tiles on the lower edge of the screen

These tiles are really just like the others, except they’ll stop a few lines short.  They’re still fully calculated, but only the visible lines are transferred.

(In hindsight, increasing the spacing between lines would help reduce the alignment and size problem here.  Adding an extra 48 bytes to each tile would allow every transfer to be optimally aligned and sized.  And would probably make no measurable difference to the total runtime.  Heck, there’s probably enough time to repack the data in local store before performing the DMA. There’s not that much…)

I started with the assumption of 128×128 pixel diamond-square tiles — they’re a power of two big (which makes them simpler to calculate), 512 bytes wide, 128 lines tall and 64KB in total size, which means two will fit in local store.

So, questions: What points outside this area are required to calculate all the points within?  How much space is required to render one of these tiles?

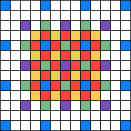(There’s a smaller example pictured, again with a different colour for each iteration of the calculation)

If the tile is to be 4×4, the centre area is 5×5 with overlap between tiles.  Additionally, to calculate a 4×4 tile, fully calculating a 7×7 area is required, not counting the sparsely calculated pixels around the outside.

Scaling this up to 128×128 pixel tiles and it should be clear that at least 131×131 pixel area is required, not counting those extras around the outside.  How to deal with those?

One thing that is clear is that they’re sparsely filled, and that calculated values only appear on certain lines.  In fact, the number of lines required around the outside of a tile is (1+log₂n) where n is the tile width.  For the 4×4 tile pictured, three extra lines are needed on each side of the tile.  For a tile 128 lines across, 8 extra lines are needed.

So all the values to calculate a given tile can be stored in in (129+8+8)×(129+8+8) = 145×145 pixels.  Rounding up to get quadword aligned storage gives a total of 148×145×4 bytes — 85,840 bytes per tile.  171,680 bytes is a big chunk of local store, but it’s probably better to be using it for something…

Based on that, it’s not particularly difficult to generate the data for a tile.  Start the tile with its starting values (more on those in another post) in the corners of the squares (the blue ones in the picture), and then calculate the remaining points.  There’s some special cases required for each of the sides, but it’s nothing particularly tricky, just keeping track of row/column indexes for particular iterations.

The outer points make up only a very small percentage of the total points that need to be calculated — more than 50% of the points are calculated in the last diamond and square iterations, and due to the proximity and alignment of the points accessed, their calculation can be usefully optimised.  (I might write a post about that sometime…)

To work out a suitable way to divide a 1080p screen into pieces that a SPU could work effectively with for the diamond-square problem took some trial and error.  First, some fundamentals.

DMA

The SPU interacts with the framebuffer through the use of DMA operations, which have the following characteristics:

• larger transfers are more efficient than smaller ones
• there are alignment constraints
• there can be a tradeoff between performing several small transfers to cope with DMA size/alignment constraints, and fetching a larger aligned area, modifying it and writing it back
• modifying a region of memory requires a DMA get and put operation — extra work, complexity (buffer management and time)
• a single SPU can have a maximum of 16 transfers in-flight at a given time, and will block if any more are issued
• DMA lists can be used to effectively issue more than 16 transfers at a time, but there are greater restrictions on the placement of data in local store

Data relationships

To calculate each point in diamond-square required the values from four others.

When calculating the centre point of a square, the four corners are located on two different lines and the centre point is written to the centre line between those two.  (Reading from two lines, writing to one)

When calculating the centre point of a diamond, the four corners are located on three different input lines and the centre point is located on the same centre line as two of the points (Reading from three lines, writing to one of those)

For a given iteration of diamond-square, all input data has been generated in a previous iteration — that is, no point depends on another point calculated in the same iteration of the algorithm.  This gives some flexibility as to the ordering of point calculation.

First attempt — whole lines

My first thought was to optimise for DMA throughput: large transfers are much more efficient than smaller ones, and the independence of points in a single iteration means that points can be calculated on a line by line basis.  Pseudo this:

square(line_number, square_size)
    top = dma_get(line_number)
    centre = dma_get(line_number + square_size/2)
    bottom = dma_get(line_number + square_size)
    for(i = 0; i < line_length; ++i)
        calculate_square_centre_value(top, centre, bottom, i, square_size)
    dma_put(centre)

Whole lines are fetched, which is reasonably efficient (1920×4 bytes = 7680, 7680%128 = 0, so it’s a fine size for efficient DMA), and there’s plenty of scope for optimisation:

• lines may be prefetched
• lines may be reused between iterations: the bottom line for one row of squares is the top line of the next.  For diamonds, two lines are reused from one row to the next

I spent quite a bit of time on this approach, to try and get it working to my satisfaction, but in the end I discarded it.  The problem for me became one of complexity — the prefetches, special cases (sides, corners) and line reuse were all written and applied for the general-case implementation (i.e. parameterised by square_size like the pseudo code above). This made it extraordinarily cumbersome to write optimised cases for the smallest square sizes — where most of the pixels are calculated and thus most runtime is spent.

In summary, I was optimising the wrong things.

There were also aspects of the implementation that I had not fully considered with this method, and failed to make progress with, particularly proper handling of the side and corner special cases, and animation.

(In hindsight, I suspect I could have simplified this approach, solved the other problems and met the time budget — but probably only knowing what I know from my next attempt.)

Second attempt — tiles — problems

Tiling was an approach I had considered and discarded early on.  Where whole lines are a clear win for DMA efficiency, tiles are much less so — the largest square tiles I could envision were 128×128 pixels, being 64KB (twice for a double buffered implementation), and the 512B line length is not a great performer.  Additionally, the limit on the number of in-flight DMA transfers makes this method seem more risky — writing 128 lines per tile requires writing lines as the calculation of each is completed and hoping that computation is slower than DMA, which is probable but not assured.

DMA lists are promising — except that diamond-square requires 2ⁿ+1 pixel squares, so it’s actually a 129×129 pixel tile (for calculation), and DMA lists still need to transfer those little extra inner parts between transfers.

On top of that, recall that diamond-square requires a large number of points from outside a tile to be calculated to be able to complete the points within a tile — if stored sparsely, 8 times as much space as for the target tile.

So I didn’t start with this idea, but after discarding the previous approach I was able to work out ways around these problems and implement a basic and functional implementation in the time I spent flying and waiting in airports on my way home from GCAP.  I’ll expand on the implementation in a later post.

or “How I got 1080p 60Hz diamond-square plasma from a single SPU”

I am primarily writing this — and subsequent posts — as a record and exercise for myself, and in case there’s anyone who attended the TUCS talk I gave in October that is still interested in the problem and my solution.

I started with a simple (naive) equation:
3.192×10⁹ cycles / (1920×1080 pixels × 60 frames per second) = 25.66 cycles per pixel

That is, to update a 1080p screen at 60Hz, there’s an upper limit of 25 cycles per pixel.

So, what can you do in 25 cycles?

Starting with the simple and obvious: On an SPU, writing to local store takes 6 cycles — that’s a quarter of the time budget gone, right there. DMAing that pixel to the framebuffer in system memory will take hundreds of cycles. Approaching this problem one pixel at a time is clearly not the way to solve it.

Slightly less simple: A write to local store will be six cycles, and it can be pipelined to give four pixels per cycle. A single SPU can do DMA at over 16GB/sec. This should be easy — and it is if all you want to do is write stuff to memory. Throw in some computation and data dependencies and things get a lot more interesting.

So, I chose a problem that is one of my old favorites from Amiga demo days — plasma. There’s a number of ways you can achieve the effect. I chose diamond-square interpolation, which turned out to have some interesting problems to implement for SPU¹.

The Diamond-Square Algorithm

The images here show the process of interpolation used for diamond-square (in these diagrams, each interpolation iteration is displayed with a different colour, not the expected calculated colour):

• Starting with one or more squares, average the corners (with a random perturbation) of the square to calculate the centre point
• For the diamonds then created, average the corner points (again, with a random perturbation) to calculate their centres
• Later, rinse, repeat until all the gaps are filled.

Seems simple enough, but there’s some complexity in the implementation.

Data points and space requirements

For a 9×9 starting grid with 9 points defined, only the innermost 3×3 square is fully filled in. The remaining un-coloured (white) points cannot be calculated without having more starting values available (or using some other special case method to appropriately generate the missing information).

Additionally, it can be seen that generate a 3×3 completed pixel region requires the full 9×9 are to start with. Not particularly space efficient.

Data dependency

To calculate a point requires the points around it to be fully calculated, and each of those requires the four surrounding it.  This also has consequences when considering how to divide the problem when trying to calculate a large bitmap using a single SPU and its 256KB local store.

Animation

Producing the same image 60 times a second is not very interesting, so there should be some way to cause it to change over time, in some continuous fashion, where each frame relates to the last in a visually pleasing fashion. Doing this in practice becomes a question of where the source “random” values come from, and how they can be varied over time.  Additionally, the use and generation of source values relates to how the output space is divided.

I’ve written previously about some of the issues I encountered when writing this (fast averaging, system calls, poorly performing first frame), and I intend to write about the three areas mentioned above (space requirements, data dependency and animation).

¹Additionally, there’s better ways to create the plasma effect. I did it all again, I’d start with Perlin noise, which appears to still have some interesting challenges but is overall better suited to the hardware.